Chapter 3: Answers 4 Jack K. Cohen Colorado School of Mines
- Use and if you still don't see the light, ask your friends or the instructor for help.
- Use the fact that
D sin x = cos x to find the derivatives of the following functions:
-
D sin(x3) = cos( ... )⋅D( ... ) = cos(x3)⋅Dx3 = 3x2cos x3.
-
D(sin x)3 = 3( ... )2⋅D( ... ) = 3(sin x)2⋅D sin x = 3 sin2x cos x.
-
D sin(sin x) = cos( ... )⋅D( ... ) = cos(sin x)⋅D sin x = cos(sin x)cos x.
-
D sin(sin(sin x)) = cos( ... )⋅D( ... ) = cos(sin(sin x))⋅D sin(sin x) = cos(sin(sin x))cos( ... )⋅D( ... ) = cos(sin(sin x))cos(sin x)⋅D sin x = cos(sin(sin x))cos(sin x)cos x. (Whew!)
- The area of a circle in terms of the radius is
A = πr2.
-
 =
= 
 = 2πr
= 2πr .
.
- (3.3.49)
 = 2πr
= 2πr = 2π⋅10⋅2 = 40π cm2/sec.
= 2π⋅10⋅2 = 40π cm2/sec.
- From part (a),
 =
= 
 . Use
r =
. Use
r = 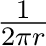 and simplify to get
and simplify to get
 =
= 
 .
.
- (3.3.50)
-
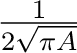 /15 cm/sec.
/15 cm/sec.
 =
= 
 = 2πr
= 2πr .
.
 = 2πr
= 2πr = 2π⋅10⋅2 = 40π cm2/sec.
= 2π⋅10⋅2 = 40π cm2/sec.
 =
= 
 . Use
r =
. Use
r = 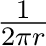 and simplify to get
and simplify to get
 =
= 
 .
.
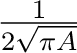 /15 cm/sec.
/15 cm/sec.